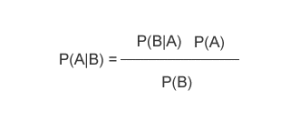Un tentativo di aggirare i problemi dell’induttivismo, rimanendo in un orizzonte di tipo empiristico è quello del cosiddetto approccio bayesiano (estratto da Giorello da raddrizzare), che cerca di avanzare un criterio in qualche modo oggettivo di valutazione del grado di verosimiglianza di una teoria (dunque anche della sua progressività). Si tratta di “misurare” la maggiore o minore verisimiglianza di una teoria attraverso il calcolo delle probabilità (ricorrendo al teorema di Bayes).
Per la precisione secondo l’approccio bayesiano una teoria h risulta tanto più verosimile quanto maggiore è la differenza tra le sue probabilità iniziali p(h) e le sue probabilità finali p(h|e) alla luce del verificarsi di una determinata evidenza e. Per probabilità iniziali si intendono le probabilità che la teoria sia vera prima di uno o più controlli empirici (e), per probabilità finali si intendono le probabilità che la teoria sia vera dopo questi controlli. Il teorema di Bayes rende conto del fatto, intuitivo, che lo scarto tra probabilità iniziali e finali di una teoria è tanto maggiore quanto minori sono le probabilità p(e) che si verifichino determinate sue conseguenze empiriche e (a condizione, ovviamente, che poi queste conseguenze effettivamente si verifichino, dal momento che, in caso contrario, per il modus tollens, la teoria sarebbe immediatamente falsificata):
p(h|e) = p(e|h)p(h)
p(e)
Il grado di verosimiglianza (V) di una teoria sarebbe dunque espresso dalla seguente relazione:
V = p(h|e) – p(h)
Popper, osservando che la probabilità iniziale che si può assegnare a una teoria prima di qualsivoglia controllo è pari a zero (il che, però, azzera il valore di V nella relazione sopra richiamata, rendendola non significativa), corregge questo approccio prendendo in considerazione il rapporto tra teoria e conoscenza di sfondo. Un controllo C può dirsi tanto più severo e la corrispondente teoria tanto più corroborata (non verificata), quanto più l’evidenza (e) che esso accerta è probabile alla luce della teoria h da corroborare e quanto meno essa è probabile alla luce della sola conoscenza di sfondo k (ossia alla luce di ciò che era già noto prima):
C = p(e|h & k) – p(e|k)
Ad esempio che la traiettoria dei fotoni sia curvata in presenza di masse gravitazionali (e) è incongruente con la legge di Newton (conoscenza di sfondo k), dal momento che secondo questa legge l’attrazione gravitazionale si esercita solo su masse, mentre i fotoni hanno massa nulla; d’altra parte tale evidenza (e) è prevista della teoria della relatività generale (h): pertanto la probabilità di e alla luce di k è zero, mentre la probabilità di e alla luce sia di k sia di h è 1 (se Einstein ha ragione, i fotoni devono necessariamente comportarsi in quel modo, mentre molti altri eventi continuano a essere compatibili con la teoria di Newton). Pertanto il controllo (C) della teoria di Einstein consistente nell’osservare il comportamento dei fotoni in presenza di masse gravitazionali è massimamente severo (la somma algebrica dell’equazione precedente dà come risultato 1). Se, invece, volessi controllare la teoria di Einstein misurando l’accelerazione di gravità al livello del mare (e), poiché tale misura (9,81 m / sec^2) è compatibile sia con la conoscenza di sfondo (k), cioè con la teoria di Newton, sia con l’ipotesi nuova (h), cioè con la teoria di Einstein, tale controllo sarebbe privo di valore (la somma algebrica dell’equazione precedente darebbe 0).
Si tratta, dunque, di un altro modo di distinguere tra esperimenti inutili ed esperimenti cruciali, quelli cioè in grado di decidere quale di due teorie sia la migliore (qui reinterpretate rispettivamente come una teoria nuova e una “conoscenza di sfondo”).