La scienza, con la rivoluzione epistemologica che si annuncia nel primo Novecento (relatività, meccanica quantistica), cessa, dunque, di essere etimologicamente “scienza” (sapere), per rivelarsi piuttosto qualcosa di diverso (costruzione ipotetica, probabilistica?, sarà l’epistemologia del Novecento a interrogarsi su tutto questo).

Si conferma, così, l’intuizione platonica esposta nella “teoria del segmento” proposta dal VI libro della Repubblica: le scienze della natura, in quanto si fondano su ipotesi piuttosto che su principi, non sono necessariamente vere, ma semmai verosimili. Le teorie scientifiche restano tali finché salvano i fenomeni (“fino a prova contraria”, come diceva lo stesso Newton in una prospettiva empiristica), altrimenti vanno sostituite o corrette: al sistema tolemaico è così subentrato quello copernicano, alla teoria di Newton è potuta subentrare la teoria della relatività ecc.

Tuttavia, dal tempo dei Greci fino all’Ottocento molti credevano che almeno il linguaggio matematico, in cui le teorie scientifiche venivano scritte, fosse incontrovertibile, assolutamente certo, perché fondato sull’evidenza di assiomi e postulati come quelli esposti negli Elementi di Euclide. Cartesio, come Leibniz e altri moderni razionalisti, aveva perfino sperato di fondare la stessa fisica su un analogo principio di evidenza (riducendo così la fisica a geometria).

Con la scoperta, tuttavia, delle geometrie non euclidee di Lobačevskij e Riemann si comincia a dubitare dell’evidenza di quella  geometria a cui si sperava di ridurre le altre scienze. Non appare più così necessariamente evidente che per un punto fuori da una retta possa passare una e una sola retta parallela alla retta data (V postulato di Euclide). Anzi, se è vera la teoria della relatività, parrebbe che lo spazio fisico, reale, obbedisca alla geometria ellittica di Riemann (secondo cui non esistono rette parallele e lo spazio è strutturalmente “curvo”) piuttosto che a quella di Euclide, che si rivela allora il frutto (non meno delle geometria di Lobačevskij) di una pura ipotesi astratta.

Si rovescia, così, la prospettiva riduzionistica: non sembra che sia tanto la fisica a dover essere geometrizzata quanto la geometria a dover essere “fisicizzata” (nel senso che è l’applicabilità ad oggetti propri della scienza fisica che deciderebbe della “fecondità” o meno di un determinato modello matematico).

Se la matematica non può più fondarsi sulla pretesa evidenza degli assiomi, “abbassati” a mere ipotesi sostituibili con altre qualsiasi (come aveva già intuito Platone), la speranza è che la matematica possa “difendere” almeno un linguaggio logicamente coerente e formalmente ineccepibile (programma di Hilbert), che possa, anzi, essere esteso a tutte le scienze per garantire, se non la loro verosimiglianza, almeno la loro interna coerenza (o, come anche si dice, consistenza), salvo poi verificare (problema di altra natura) se le teorie così costruite  “salvino” o meno i fenomeni. Quanto meno tali teorie “scientifiche”, vere o false che si rivelino, si distinguerebbero da “chiacchiere da bar” o da credenze non scientifiche per essere costruite attraverso un procedimento coerente, logico-matematicamente garantito.

Ecco il senso epistemologico del tentativo di ridurre la matematica alla logica (logicismo). Se la matematica non può più fondarsi sull’intuizione geometrica, forse – ci si augura – potrà fondarsi su una logica incontrovertibile.

Per raggiungere questo obiettivo si tenta, in primo luogo, la riduzione della geometria (non più giustificabile su basi intuitive, cioè legate all’evidenza) a un’aritmetica adeguatamente “assiomatizzata” (logicizzata, attraverso la teoria degli insiemi di Cantor e Frege).

Per comprendere meglio questo passaggio si può chiarire meglio il senso del tentativo di Cantor di “saturare il continuo”. Egli tenta di aritmetizzare la geometria, mostrando come “tradurre” un segmento in un insieme di coordinate (relative agli infiniti punti costituenti il segmento) esprimibili ricorrendo a un determinato insieme transfinito (di potenza o cardinalità 2) di decimali compresi da 0 a 1 (numeri razionali).

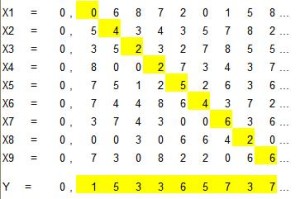
Per ottenere questo risultato (ossia per generare un insieme infinito di cardinalità 2 da un insieme infinito di cardinalità 1) egli deve scoprire come sia possibile costruire un insieme infinito di numeri non compresi in un altro insieme infinito di numeri, compresi nel medesimo intervallo (0-1). A questo fine egli procede come segue. Data una tabella contenente infiniti numeri decimali sovrapposti, compresi tra 0 e 1 e caratterizzati da un numero infinito di cifre ciascuno, se ne ricavi il numero decimale j che risulta costituito, “diagonalmente”, dalla prima cifra decimale del primo numero, dalla seconda del secondo, dalla terza del terzo e così via. Si costruisca poi un numero k aumentando di un’unità ogni cifra decimale del numero j (e cambiando ogni 9 in uno 0). È facile accorgersi che il numero k non può, per costruzione, essere uno dei pur infiniti numeri contenuti nella tabella, perché se così fosse quella delle sue cifre (in un’ennesima posizione, quale che sia) “raccolta” dalla diagonale non sarebbe stata aumentata di 1. Questo numero k è il “primo” degli infiniti numeri costruibili col “metodo della diagonale”. Secondo Cantor tali infiniti numeri, eccedenti il primo insieme (quello corrispondente alla tabella), consentirebbero di saturare un continuo, esprimendo le coordinate di tutti i punti che lo costituiscono (del tutto indifferentemente che tale continuo, purché di dimensioni finite, sia espresso da un segmento, da una superficie o da un volume). Purtroppo questo approccio di Cantor non consente, però, di distinguere i tipi di “infinito” che intervengono nello sviluppo delle dimensioni spaziali (l’infinità dei punti che costituiscono un segmento di misura x è della stessa cardinalità o potenza all’infinità dei punti che costituiscono un quadrato dall’area x²).

Come si vede, Cantor, per (tentare di) aritmetizzare la geometria, deve anche “logicizzarla”, valendosi dell’insiemistica (una creazione sua e di Frege). Ora, se la logica fosse stata un sapere incontrovertibile, tale operazione avrebbe potuto conseguire il risultato sperato: la messa in luce dei fondamenti certi della matematica e, con questa, di tutto l’edificio delle scienze cosiddette “esatte” (a prescindere dal problema della loro verifica sperimentale).

Purtroppo con la scoperta dell’antinomia degli insiemi di Russell (che evoca tutta una “tradizione” di antinomie ben note alla filosofia, dai paradossi di Zenone al paradosso megarico “Io mento”, dalle aporie dell’uno nel Parmenide di Platone alla dialettica del Principio in prospettiva neoplatonica, dalle antinomie della ragion pura in Kant alla dialettica di Hegel) il programma del logicismo fallisce (e con esso anche quello del riduzionismo positivistico), riconsegnando alla filosofia e, specialmente, all’epistemologia il problema di “perimetrare” in qualche modo il  sapere scientifico (a cominciare dalla matematica stessa), distinguendolo dalle “pseudoscienze”. L’antinomia di Russell consiste in questo: l’insieme di tutti gli insiemi che non includono se stessi non può né includere, né non includere se stesso, il che, per il principio di non contraddizione (e del terzo escluso), è assurdo.

Dunque la teoria degli insiemi permette di costruire “oggetti” assurdi.

L’antinomia di Russell è aggravata successivamente dai teoremi di Goedel (1931). Il (doppio) teorema di Goedel richiederebbe una trattazione logico-matematica, ma si può semplificare come segue.

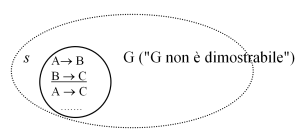
Dato un sistema (s) assiomatizzato (ossia riducibile ad assiomi e a teoremi dimostrabili a partire dagli assiomi, il tutto espresso in un determinato linguaggio, p.e. quello dell’aritmetica), purché il sistema ammetta proposizioni che possano riferirsi anche a se stesse (come è tipico di ogni sistema logico che sia di qualche interesse), è sempre possibile scrivere una proposizione vera, nel linguaggio del sistema, che, tuttavia, resta indecidibile, cioè indimostrabile nel sistema medesimo. Ad esempio la proposizione G, il cui contenuto è “G non è dimostrabile” (o “io non sono dimostrabile” o “questa stessa proposizione non è dimostrabile”), è vera se, appunto, non è dimostrabile. Infatti, se, ad esempio considerassi il ragionamento, che mi ha appena fatto concludere che G è vera, una dimostrazione di G, allora G sarebbe falsa. In altre parole, se il sistema dimostrasse G, esso diventerebbe incoerente (perché dimostrerebbe e confuterebbe nello stesso tempo G). Diventando incoerente, in esso si potrebbe dimostrare tutto e il contrario di tutto, per il principio scoperto già dai logici medioevali ex absurdo quodlibet (da ciò che è contraddittorio segue qualsiasi cosa). Ad esempio in un’aritmetica in cui 0 = 1, tutti i numeri sarebbero uguali a tutti i numeri e i risultati di tutte le operazioni, indistinguibili tra loro, sarebbero veri e falsi insieme. Affinché il sistema non diventi incoerente G deve, dunque, rimanere indimostrabile. Tuttavia, in questo caso il sistema sarebbe coerente, ma incompleto, cioè ammetterebbe infinite proposizioni indecidibili, espresse nel linguaggio del sistema. In compenso sappiamo che s è coerente se G è vera. Infatti G può restare indimostrabile solo se non vale il principio medioevale ex absurdo quodlibet, altrimenti G (come anche non-G) verrebbero dimostrate dal sistema, in quanto incoerente. Dunque se G è indimostrabile come dichiara di essere, allora s deve essere coerente.

In ultima analisi Goedel dimostra irrefutabilmente che un sistema di proposizioni logicamente connesse (quale è o aspira ad essere anche una teoria scientifica, non solo matematica), se spera di essere coerente, deve necessariamente restare incompleto (nel caso di un teoria scientifica, vi saranno sempre proposizioni espresse nel linguaggio della teoria, concernenti p.e. determinati “oggetti fisici”, che non possiamo decidere se siano vere o false restando all’interno della teoria stessa). Se il sistema tenta di diventare completo, automaticamente diventa incoerente.

Questo implica, in ultima analisi, che, data una certa teoria, non possiamo sapere, restando “dentro” la teoria, se essa sia  coerente o meno. Possiamo valutarne la coerenza utilizzando un’altra teoria (p.e. utilizzando il linguaggio naturale per discutere una certa interpretazione dell’aritmetica), ma poi si dovrebbe valutare la coerenza della teoria sovraordinata alla prima e così via all’infinito. Dunque nello sviluppo di una certa teoria (o nell’esecuzione di un certo programma) possiamo sempre imbatterci in antinomie e paradossi (o bugs) dove meno ce lo aspettavamo, senza che possiamo prevederlo in anticipo con certezza.

Un esempio chiaro delle difficoltà che tutto questo comporta può venire dal tentativo di Russell, nei suoi Principia mathematica, di ovviare all’antinomia da lui stesso scoperta. Per impedire l’insorgere di antinomie in una teoria Russell propone che la determinata teoria non possa mai contenere concetti che si riferiscono a se stessi o ad altri concetti della teoria medesima (come il concetto di “insieme che contiene se stesso”, oppure proposizioni che si riferiscono a se stesse); cioè vieta ogni forma di autoreferenzialità. Per parlare dei concetti espressi in un certo linguaggio (p.e. aritmetico), occorre adottare un altro linguaggio di livello superiore (metalinguaggio, p.e. la lingua italiana) e così via. Bene, la domanda ora è: “Questa stessa teoria dei tipi o dei metalinguaggi rispetta questa regola?”. Si direbbe di no: infatti per occuparsi “senza incidenti” di ciò di cui si occupa (cioè ogni altra teoria) dovrebbe costituire un “metalinguaggio” rispetto alle altre teorie, ma, dal momento che essa stessa si occupa proprio di “metalinguaggi”, essa sarebbe (autoreferenzialmente) uno degli oggetti di cui si occupa, proprio quello che una teoria non dovrebbe essere; d’altra parte, invece, se essa non fosse formalmente sovraordinata a ogni altra teoria come un metalinguaggio, rimarrebbe esposta a tutti i paradossi e le antinomie che già conosciamo.