Proviamo a seguire storicamente l’evoluzione della scienza (in senso platonico), prestando particolare attenzione all’astronomia, ossia l’ambito della “matematica” antica le cui trasformazioni hanno inciso maggiormente negli sviluppi della scienza nel suo complesso (a cominciare da ciò che oggi chiamiamo “fisica”).

L’astronomia del mondo classico nasce sostanzialmente geocentrica. Si noti che l’intuizione che la Terra sia rotonda, immobile al centro dell’universo, costituisce già una profonda innovazione. Le apparenze (i “sensi”), infatti, ci suggeriscono che la Terra sia piatta, in conformità a quanto “sapevano”, prima dei Greci, Egizi, Sumeri, Babilonesi, Ebrei, Indiani, Cinesi ecc.  Solo il ragionamento ci fa ritenere che essa possa essere sferica, considerando che, quando guardiamo le navi giungere dal mare, prima ne vediamo gli alberi e solo dopo lo scafo.

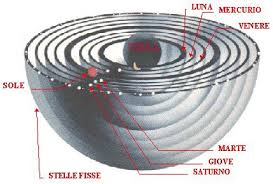
L’antico modello cosmologico geocentrico prevede un ordinamento dei pianeti dalla Terra a Saturno, corrispondenti ad altrettanti “cieli” o “sfere celesti”  (la sequenza dalla Terra è precisamente:  Luna, Mercurio, Venere, Sole, Marte, Giove, Saturno), ed è alla base della nostra “settimana lunare“, eredità del tardo impero romano. Se associamo, infatti, ciascuna delle 24 ore di ogni giorno a una pianeta nella sequenza inversa (da Saturno alla Luna),  iterando quest’ultima (cfr.  origine della settimana), ogni nuovo giorno inizia con un’ora associata al pianeta che è precisamente quello che ancora lo denomina: lunedì, martedì ecc.. (cfr. anche la giustificazione “a stella” della sequenza dei giorni della settimana sulla base del suddetto ordinamento planetario).

Nondimeno il modello geocentrico presenta difficoltà considerevoli, poiché, sebbene tutti i corpi celesti partecipino dell’apparente rotazione diurna intorno alla Terra, le posizioni relative di alcuni astri nella volta celeste mutano attraverso i giorni, i mesi, gli anni.

Il Sole e la Luna, ad esempio, si spostano ogni giorno rispetto allo sfondo delle c.d. “stelle fisse” nella medesima direzione (impiegando rispettivamente un anno e un mese a fare l’intero giro) lungo la fascia celeste immaginaria denominata “zodiaco” (quella che accoglie la sequenza delle costellazioni zodiacali: Ariete, Toro, Gemelli ecc., che al tempo dei Babilonesi identificavano via via la posizione nella quale si trovava il Sole nel corso dell’anno). Altri astri, le cosiddette “stelle erranti” (planetài), cioè i cinque pianeti visibili a occhio nudo (Mercurio, Venere, Marte, Giove e Saturno, associati ad altrettanti dèi), oltre a muoversi lungo lo zodiaco (lett. la “fascia degli animali”, zòa, cioè appunto queste stesse stelle erranti), come fanno il Sole e la Luna, sono contraddistinti anche da moto retrogrado e da variazione di luminosità: il che si spiega con difficoltà immaginando la Terra immobile.

Risalendo dunque alla prima metà del IV secolo, il primo tentativo sistematico (certo) di fornire una spiegazione di questa apparente irregolarità di moti planetari fu quello dovuto a Eudosso di Cnido, astronomo dell’Accademia di Platone (che probabilmente riprende precedenti ipotesi pitagoriche). Sì tratta di un modello puramente geome­trico, il cui intento non è quello di descrivere quali realmente siano i moti dei corpi celesti, bensì quello di salvare i fenomeni, in senso platonico (procedura ipotetico-deduttiva tipica di ciò che i Greci intendevano per “matematica”), cioè di fornire una composizione geometrica ideale di moti che riproduca ciò che noi vediamo accadere nella volta celeste. Si tratta dell’atto di nascita della scienza, come la intendiamo ancor oggi: non semplice somma di osservazioni o di descrizioni di fatti, ma una loro interpretazione (matematica) basata su ipotesi (relative ad entità invisibili, come per noi sono gli atomi o i campi di forze) introdotte per “rendere ragione”, “spiegare”, “salvare” ciò che i sensi percepiscono.

Eudosso, pertanto, scompone il moto apparentemente disordinato dei diversi corpi celesti in una combinazione di più moti circolari uniformi. Il moto circolare era già stato additato infatti come moto perfetto dai Pitagorici e da Platone. Eudosso immagina pertanto che ciascun pianeta possa fingersi collocato nell’equatore di una sfera ideale ruotante intorno a un asse incernierato in una seconda sfera, fornita anch’essa di un moto rotatorio intorno a un altro asse inclinato rispetto al primo, e così via fino ad un massimo di quattro sfere. Per il moto delle stelle fisse è sufficiente una sola sfera, per il Sole e per la Luna se ne richiedono tre, per gli altri pianeti (planetài, cioè stelle erranti) quattro. Il comporsi di tali moti circolari riproduce con una certa approssimazione ciò che osserviamo nel cielo.

Nel modello di Eudosso permangono, nondimeno, all’osservazione talune ano­malie inspiegabili, consistenti soprattutto in variazioni di luminosità che fanno pensare a variazioni di distanza (soprattutto nel moto della Luna, di Mercurio, di Venere e di Marte). Ciò induce a cercare spiegazioni più soddisfacenti correggendo il modello geocentrico, o abbandonandolo del tutto, se­condo un indirizzo già delineato nella scuola pitagorica, o, infine, proponendo soluzioni intermedie.

Prima di esaminare l’intuizione geniale di Aristarco di Samo (che, per primo, propose un modello eliocentrico, ripreso nel Cinquecento da Copernico), consideriamo i tentativi di “salvare” il modello di Eudosso, da parte di Ipparco e Tolomeo.

Nel farsi sostenitore del modello geocentrico Ipparco (II sec. a. C.) cerca di renderlo più ri­spondente alle osservazioni empiriche facendo ampiamente ricorso a due ingegnosi meccanismi, le sfere eccentriche e gli epicicli. Non sappiamo chi per primo li propo­nesse; sappiamo comunque che erano già noti ad Apollonio e che furono escogitati probabilmente all’inizio del III sec. a.C..

Le sfere di Eudosso hanno tutte il loro centro nel centro della Terra. Attraverso il modello degli eccentrici si propone invece che il centro delle sfere si collochi in un punto posto sulla retta che congiunge la Terra al Sole; pertanto il centro dell’orbita eccentrica non è fisso, ma descrive esso stesso un’orbita circolare intorno alla Terra. Si tratta, in sostanza, di un’orbita su di un’orbita. In tal modo i pianeti variano periodicamente, non solo la posizione rispetto agli altri corpi celesti, ma anche la loro distanza dalla Terra; il che spiega il variare del diametro della Luna e, soprattutto, il variare della luminosità dei pianeti (problema lasciato irrisolto dal modello di Eudosso-Aristotele), particolarmente sensibile per Venere e Marte.

Cfr. quest’animazione.

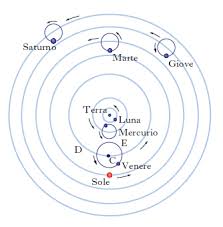
Equivalente da un punto di vista geometrico è la teoria degli epicicli. In questa il pianeta percorre un’orbita circolare secondaria, detta epiciclo, intorno ad un punto, che a sua volta descrive l’orbita primaria, detta deferente, che ha come centro la Terra. Anche qui, pertanto, un’orbita il cui centro si colloca su di un’altra orbita. L’unica differenza sta nel fatto che nell’eccentrico ambedue le orbite racchiudono nel loro giro la Terra, mentre invece nel secondo procedimento la Terra è circondata solo dal deferente e non dall’epiciclo, che ha un raggio molto più corto del deferente

Al modello geocentrico fornisce definitiva sistemazione Claudio Tolomeo, vissuto ad Alessandria nel Il secolo d.C. Si occupa, oltre che di astronomia, di matematica, di fisica e di astrologia. La sua opera fondamentale, Sintassi matematica, in 13 libri, successivamente chiamata La Massima (in greco He meghìste, donde il nome arabo Al­magesto), accoglie e rielabora coerentemente la molteplicità delle osservazioni, dei calcoli e delle ipotesi sul moto dei corpi celesti. Alla messe dei dati raccolti dai precedenti astronomi, Tolomeo aggiunge quelli provenienti dalle sue osservazioni dirette, e riordina tutto il materiale con raffinati strumenti matematici, facendo am­pio uso dei procedimenti già utilizzati da Ipparco. Attraverso il poderoso apparato di dati e di ipotesi, Tolomeo rende possibile stabilire quelle tavole, che sono anche oggi tra i compiti dell’astronomia, e che permettono dì calcolare per ogni istante, passato o futuro, la posizione dei corpi celesti.

Tuttavia, anche il modello di Tolomeo presenta problemi. Esso, ad esempio, non ammette un’interpretazione fisica, se seguiamo la dottrina aristotelica del moto. Per tale dottrina il vuoto è impossibile. Se lo fosse, i corpi mossi da una forza piccola a piacere, in assenza di resistenza, acquisterebbero velocità infinita. Ma i pianeti, che nel modello di Tolomeo si muovono necessariamente nel vuoto (altrimenti non potrebbero percorrere gli epicicli), si spostano a velocità finita…