
Supponiamo, dunque, che tutto sia “codificato” in una sorta di “lastra olografica cosmica” (l’ordine implicato di cui parla David Bohm o, se preferisci, il “campo di punto zero” della fisica dei quanti), al di fuori dello spazio e del tempo, coincidente con il “cosmo noetico” dei platonici e con l’Uno senza secondo di Parmenide e dei neo-platonici. Tale “lastra” conterrebbe tutte e sole le informazioni necessarie a generare l’ologramma in cui l’universo (l’ordine esplicato di Bohm) ci appare (il “mondo sensibile”) o, per meglio dire, appare alla coscienza (a ciascuno di noi, di volta in volta). Alla coscienza appare, infatti, l’universo in tre dimensioni spaziali e nel tempo (che scorre solo nella coscienza).
Le regole (leggi, algoritmi) che determinano come l’ordine implicato si proietti qui e ora nell’ordine esplicato sono inflessibili. Per questo parliamo di ordine. Anche se tutto si svolge nella coscienza non siamo “liberi” di volare o di vedere un cerchio quadrato.
- Dunque vige il più stretto determinismo!
Ciò che è è e non può non essere. Sotto questo profilo tutto è necessario. Tuttavia, tra le regole che determinano il modo in cui tutto appare (l’ordine che si esplica nello spazio e nel tempo) ve ne dev’essere una che vieta di dimostrare in un numero finito di passi la necessità dell’ordine in quanto tale, ossia l’incontrovertibilità di tutte le regole che vincolano i modi possibili della manifestazione.
Ciò fa sì che soggettivamente anche eventi necessari appaiano contingenti. Non è possibile dedurli da principi incontrovertibili.
Ciò potrebbe fare sì, ad esempio, che non sia possibile “raddrizzare” in senso deterministico i fenomeni quantistici introducendo “variabili nascoste”,
- Puoi essere più chiaro?
Si può dimostrare per assurdo (ossia incontrovertibilmente), ad esempio, che un cerchio non può essere quadrato; in generale un certo numero di teoremi, dato un certo numero di assiomi e definizioni. Tuttavia, anche in campo matematico, alcune tesi rimangono allo stato di congetture, in attesa di dimostrazione. D’altra parte esse si rivelano estremamente probabili su base empirica (finora i fenomeni le hanno rispettate): appare, cioè, probabile che esse costituiscano alcunché di “necessario” anche se non si è ancora riusciti a dimostrarne la necessità.
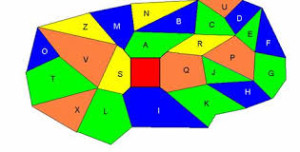 Una congettura di questo tipo è quella dei “quattro colori”, secondo la quale su una mappa piana sarebbe possibile disegnare territori di qualsiasi forma, servendosi di soli quattro colori, in modo tale che nessun territorio abbia lo stesso colore di un territorio adiacente.
Una congettura di questo tipo è quella dei “quattro colori”, secondo la quale su una mappa piana sarebbe possibile disegnare territori di qualsiasi forma, servendosi di soli quattro colori, in modo tale che nessun territorio abbia lo stesso colore di un territorio adiacente.
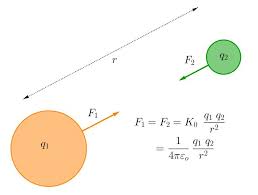 Immagina, ora, che le leggi di natura (p.e. la legge di Newton o quella di Coulomb) siano congetture in questo senso. Una mente divina potrebbe riconoscerne la necessità, ma il numero dei passi necessario a dimostrare che si tratta di leggi incontrovertibili è infinito, il che rende impossibile che una mente umana li compia.
Immagina, ora, che le leggi di natura (p.e. la legge di Newton o quella di Coulomb) siano congetture in questo senso. Una mente divina potrebbe riconoscerne la necessità, ma il numero dei passi necessario a dimostrare che si tratta di leggi incontrovertibili è infinito, il che rende impossibile che una mente umana li compia.
Tuttavia, l’esperienza della costanza di queste leggi ci suggerisce che (almeno alcune di) esse siano non semplicemente “per lo più” valide (come in una prospettiva rigorosamente empiristica), ritenute tali, cioè, solo sulla base di un’abitudine, bensì “necessarie”, sebbene tale loro necessità non sia stata dimostrata, né sia verosimilmente dimostrabile.
- D’accordo. Ma questo a che cosa ci porta?
Se ciò di cui facciamo esperienza (o di cui siamo coscienti) è determinato da regole necessarie, “ciò che è” (percepito e concepito) non potrebbe essere diverso da com’è, anche se esso ci appare come contingente. Sotto questo profilo, ciò che appare possibile, ma è di fatto qui e ora impossibile, è soltanto il pensabile, ciò che immaginiamo che possa accadere solo perché ignoriamo le regole che determinano quello che accade.
- La tua ipotesi non paga, allora, un prezzo troppo alto a una prospettiva di tipo razionalistico? Perché escludere, come suggerisce David Hume e, da ultimo, un autore a te caro, come Rupert Sheldrake (teorico dei campi morfogenetici), che tutto evolva, comprese le leggi fondamentali della fisica [p. 25 e ss.] e, – perché no? -, anche quelle della logica? In questa prospettiva solo l’abitudine ([p. 28 e ss.] custom, in Hume), derivata dall’esperienza (dei sensi), ci farebbe assumere che persista, nel tempo, “platonicamente” (direbbe Sheldrake, caricando questo avverbio di connotazioni negative, cfr. p. 34), ciò che, invece, potrebbe evolvere: il principio di conservazione dell’energia, per esempio, o le stesse leggi di natura; o, infine, – perché no? – la stessa “unità” del tutto, in quanto, almeno, scaturisce dalla nostra “logica” (a sua volta in evoluzione).
Non escludo affatto che alcune leggi di natura possano evolvere nel tempo. Secondo alcuni, ad esempio, le forze fondamentali della natura (nucleare forte e debole, elettromagnetica e gravitazionale) deriverebbero “storicamente” da una forza originaria. Mi seduce anche l’idea che l’universo stesso, in espansione, possa essere paragonato validamente a un organismo vivente [cfr. Sheldrake, p. 21, p. 356 e ss.]. Ma anche in questa prospettiva deve essere pensata come eternamente stabile, perché necessaria, almeno una “legge” (un “principio”): quella secondo la quale le cose (tutte le cose), appunto, lentamente evolvono: nell’ipotesi di Sheldrake: sulla base di “campi morfici” (o altrimenti). In ultima analisi la stessa fiducia che riponiamo in ciò a cui siamo abituati deriva, come sapeva bene l’empirista Isaac Newton, da una credenza nell’uniformità della Natura, che “non facit saltus” (come diceva Leibniz, l’avversario matematico di Newton).
In ultima analisi, sebbene tu mi possa tacciare di “razionalismo” o, peggio, di “idealismo”, resta vero che tutto quello che sfugge alla nostra logica, fondata sul principio di non contraddizione (logica per la quale non posso pensare all’uni-verso se non come uno), resta un impensabile, qualcosa di cui solo contraddittoriamente si potrebbe dire che “è” (dove “contraddittoriamente” significa: “senza che la frase in cui lo si dice possa conservare un senso per chi l’ascolta”).
- Mi stupisci! Tu stesso evochi sovente le antinomie nelle quali, seguendo il filo della nostra ragione, finiremmo (quasi) inevitabilmente per imbatterci (cfr. Platone 2.0, § 4.5.4)… L’ipotesi che tutto sia uno non è a sua volta antinomica? Lo suggerisce il fatto stesso che tu & io, che siamo due e siamo diversi, siamo qui, paradossalmente, a ragionarne…
Certo, tutto è antinomico. In generale, l’unità originaria implica, paradossalmente, come ha dimostrato una volta per sempre Platone nel dialogo Parmenide, la separazione originaria, in primo luogo: quella del soggetto dall’oggetto. Tuttavia, non si darebbe antinomia se, per così dire, mentre non possiamo fare a meno di pensare che tutto, anche, non sia uno (perché – come dici tu – siamo qui, almeno in due, a riflettervi o, più fondamentalmente, perché io stesso sono cosciente di tutto ciò che, apparentemente, io non sono), non possiamo neppure fare a meno di pensare che tutto sia uno. Cancellare quest’ultimo, fondamentale, corno del dilemma, come tentano di fare gli empiristi e gli scettici di ogni tempo, non è semplicemente possibile.
